4.3 Following up on Bernoulli
Suppose \(X\) is binomially distributed:
\[X\sim Bin(n,\theta) \\ f(x|\theta) = {n\choose x} \theta^x (1-\theta)^{n-x}\]
From the warmup, given that \(E(X)=p\), we know that
\[\begin{aligned} I(\theta) & = -E_{\theta} \left[ \frac{d^2 log f(x|\theta)}{d\theta^2}\right] \\ & = \frac{1}{\theta (1-\theta)} \end{aligned}\]
Then \(\pi_J(\theta) = I(\theta)^{\frac{1}{2}} \propto \theta^{\frac{1}{2}}(1-\theta)^{\frac{1}{2}}\), so the Jeffreys prior has the distribution of a \(Beta\left(\frac{1}{2},\frac{1}{2}\right)\) density. Below, we can see the distributions of a \(Beta\left(\frac{1}{2},\frac{1}{2}\right)\) and a \(Beta(1, 1)\), or flat prior.
x <- seq(0,1,length=200)
beta_dist <- data.frame(cbind(x, dbeta(x,1,1), dbeta(x,0.5,0.5)))
colnames(beta_dist) <- c("x","a=1 b=1","a=0.5 b=0.5")
beta_dist <- melt(beta_dist,x)
g <- ggplot(beta_dist, aes(x,value, color=variable))
g+geom_line() + labs(title="Beta Distribution") + labs(x="Probability", y="density")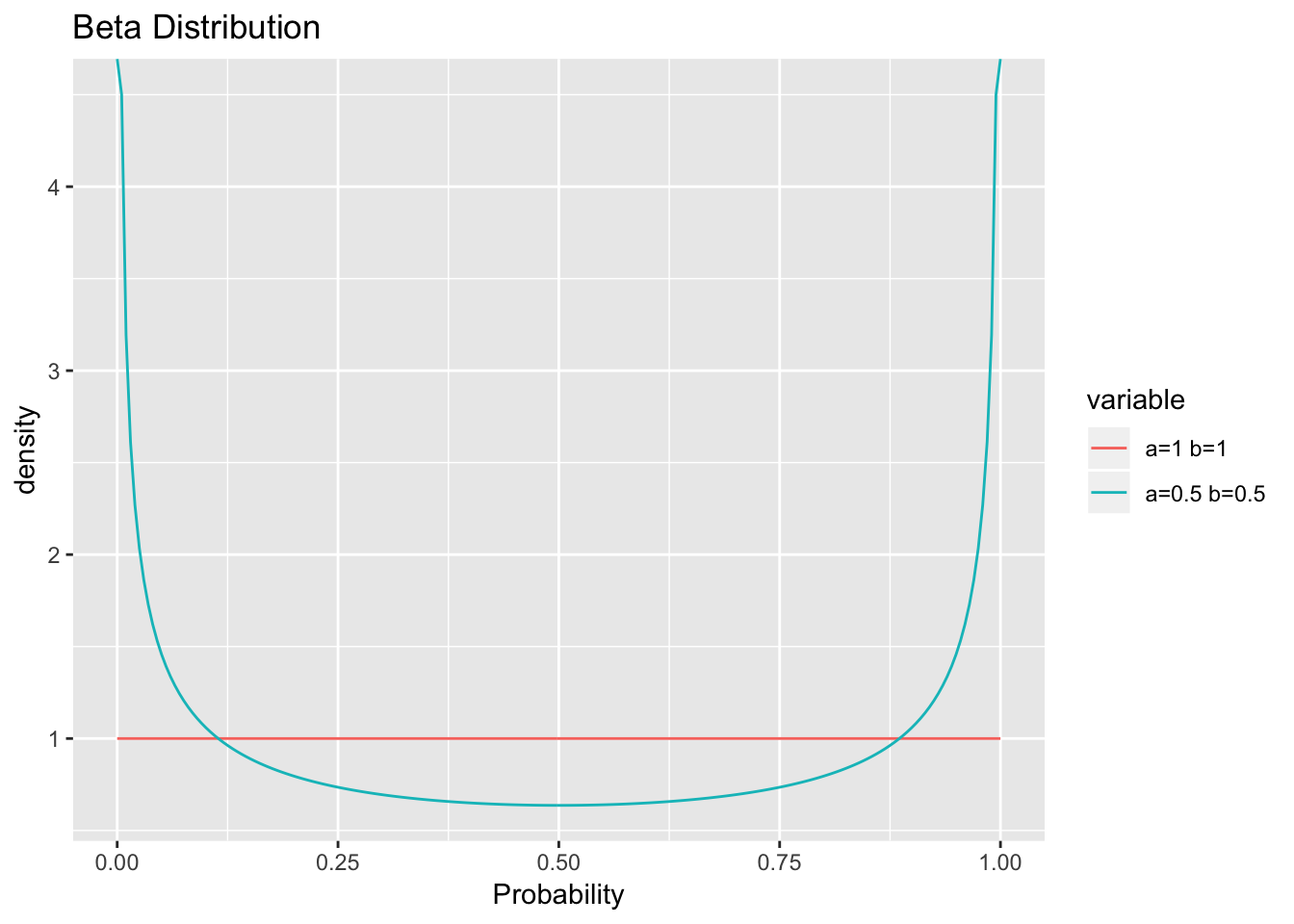
Here, we see that the Jeffreys prior compensates for the likelihood by weighting the extremes. Under the likelihood, data around \(p=0.5\) has the least effect on the posterior, while data that shows a true \(p=0\) or \(p=1\) will have the greatest effect on the posterior. The Jeffreys prior is noninformative because it weights the opposite of the likelihood function while a flat prior would not. In this case, the Jeffreys prior happens to be a conjugate prior, though this is not always true.